Physics 357 : 1998 Lecture 25

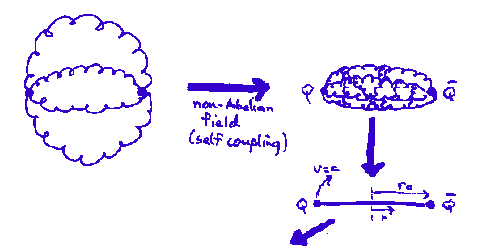
Two massless quarks connected by gluonic "string". For a potential
the mass (M) and orbital angular momentum (L) are (including both ends of the string)
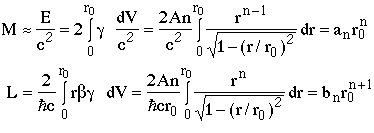
where an and bn are numerical constants depending on the value of n.
giving
where cn is a numerical constant, e.g. c1=1/Ahc.
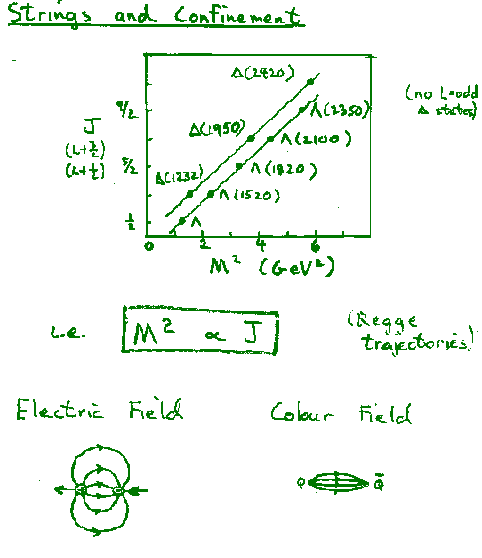
Hence the data indicate n=1 --> V=Ar
The observed potential
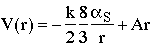
leads to quark confinement, since the string tension, A = 0.85 GeV/fm (=1.4kN~ 15 tons!), means that the string will always break and create quark-antiquark pairs if one tries to separate strongly interacting particles. i.e. quarks are confined.
This is a phenomenological potential and the string part is not, as yet, derivable from the fundamental theory of QCD, although numerical calculations and plausibility arguments suggest that QCD is in agreement with the observations.
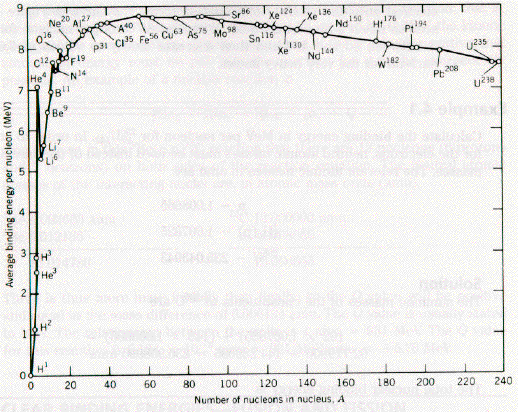
Nuclear Binding Energy per Nucleon
Semi-empirical Nuclear Mass Formula
The binding energy of an atom (Z protons & electrons, N neutrons, A=N+Z) is the difference between the summed masses of the separate nucleons and electrons and the atomic mass:
(See F&H Eqns. 16.1-3)
The net binding energy is due to several factors, but the measured binding energy per nucleon is almost constant (B/A~8MeV) for stable nuclei withA>25.
(See F&H Figure 16.1.)
This binding energies can be approximately understood as the sum of several terms.
Coulomb Energy: It takes energy to force protons together into a nucleus. We can estimate this energy by assuming that the nucleus is spherical (radius R) and that the nuclear charge (Ze) is distributed uniformly inside the nucleus. Classically the electrostatic energy the nucleus is then
If we assume nuclei are formed from incompressible nucleons with fixed nuclear bond lengths, then the nuclear volume should be proportional to A, and the nuclear radius (assuming spherical nuclei) should be
and
or
Volume Energy: Nuclear forces are short range. If we assume nuclear matter is uniform, then each nucleon will feel the same attractive nuclear force and have the same nuclear contribution to the binding energy:
Surface Energy: Nucleons at the surface are not surrounded by other nucleons so they should have less nuclear binding energy. (The forces on the surface are similar to surface tension in a liquid drop, so this force favours spherical nuclei.) If the nuclear forces are nearest neighbour forces, then the this surface contribution to the binding energy should just be proportional to the number of surface nucleons. For fixed radius nucleons, the number of nucleons at the surface should just be proportional to the surface area (4pR2~V2/3~A2/3) for a spherical nucleus) and the surface energy contribution is:
Symmetry Energy: Nucleons are fermions, so no two protons (or no two neutrons) can be in the same state. As you add nucleons to a nucleus, the nucleons must go into higher and higher energy states, with one neutron and one proton allowed to share each quantum state. Thus the Pauli exclusion principle favours nuclei with equal numbers of neutrons and protons. If we assume the nucleons in a nucleus form a cold degenerate Fermi gas, then the asymmetric nuclei pay an energy penalty:
So the total binding energy of a nucleus can be estimated by the Bethe-Weisäcker semiempirical mass formula
B = Ecoul + Evol + Esurf+ Esym
= - ac Z2/A1/3 + av A - as A2/3 - asym (Z-N)2/A
or (F&H Eqn. 16.10)
It must be remembered that this formula is only approximate. For example:
- spin-orbit couplings (F&H Section 17.3)
- closed shells are more tightly bound leading to
"magic numbers" for stable nuclei (F&H Section 17.1,2)
with N or Z =2, 8, 20, 28, 50, 82, 126.
Return to List of Lecture Notes