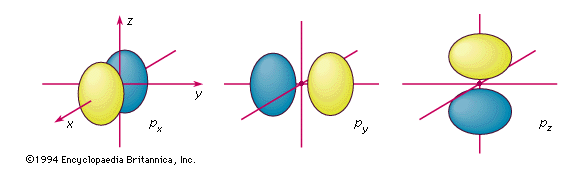Bell's Theorem
Click here
to go to the Physics Virtual Bookshelf
INTRODUCTION
In 1975 Stapp called Bell's Theorem "the most profound discovery of
science." Note that he says science, not physics. I agree with
him.
In this document, we shall explore the theorem. We assume some familiarity
with the concept of wave-particle duality; a document on this may be found here.
We also assume considerable familiarity with the Stern-Gerlach experiment and
the concept of a correlation experiment; a document on these may be found here.
A much simpler introduction to the theorem, with some loss
of completeness, has been prepared. You may access an html or pdf version
with the links to the right. |
|
The origins of this topic is a famous paper by Einstein, Rosen and
Podolsky (EPR) in 1935; its title was Can Quantum-Mechanical Description of
Physical Reality be Considered Complete? They considered what Einstein
called the "spooky action-at-a-distance" that seems to be part of Quantum
Mechanics, and concluded that the theory must be incomplete if not outright
wrong. As you probably already know, Einstein never did accept Quantum
Mechanics. One of his objections was that "God does not play at dice with the
universe." Bohr responded: "Quit telling God what to do!"
In the early 1950's David Bohm (not "Bohr") was a young Physics
professor at Princeton University. He was assigned to teach Quantum Mechanics
and, as is common, decided to write a textbook on the topic; the book is still
a classic. Einstein was at Princeton at this time, and as Bohm finished each
chapter of the book Einstein would critique it. By the time Bohm had finished
the book Einstein had convinced him that Quantum Mechanics was at least
incomplete. Bohm then spent many years in search of hidden variables,
unobserved factors inside, say, a radioactive atom that determines when it is
going to decay. In a hidden variable theory, the time for the decay to occur is
not random, although the variable controlling the process is hidden from us. We
will discuss Bohm's work extensively later in this document.
In 1964 J.S. Bell published his theorem. It was cast in terms of a hidden variable
theory. Since then, other proofs have appeared by d'Espagnat, Stapp, and others
that are not in terms of hidden variables. Below we shall do a variation on
d'Espagnat's proof that I devised; it was originally published in the American
Journal of Physics 50, 811 - 816 (1982).
PROVING BELL'S INEQUALITY
We shall be slightly mathematical. The details of the math are
not important, but there are a couple of pieces of the proof that will be
important. The result of the proof will be that for any collection of objects
with three different parameters, A, B and C:
The number of objects which have parameter A but not parameter B plus
the number of objects which have parameter B but not parameter C is greater
than or equal to the number of objects which have parameter A but not parameter
C.
We can write this more compactly as:
Number(A, not B) + Number(B, not C) greater than or equal to
Number(A, not C)
The relationship is called Bell's inequality.
In class I often make the students the collection of objects and choose
the parameters to be:
A: male B: height over 5' 8" (173 cm) C:
blue eyes
Then the inequality becomes that the number of men students who do not
have a height over 5' 8" plus the number of students, male and female, with a
height over 5' 8" but who do not have blue eyes is greater than or equal to the
number of men students who do not have blue eyes. I absolutely guarantee that
for any collection of people this will turn out to be true.
It is important to stress that we are not making any statistical
assumption: the class can be big, small or even zero size. Also, we are not
assuming that the parameters are independent: note that there tends to be a
correlation between gender and height.
Sometimes people have trouble with the theorem because we will be doing
a variation of a technique called proof by negation. For example, here
is a syllogism:
All spiders have six legs. All six legged creatures have wings.
Therefore all spiders have wings
If we ever observe a spider that does not have wings, then we know that
at least one and possibly both of the assumptions of the syllogism are
incorrect. Similarly, we will derive the inequality and then show an
experimental circumstance where it is not true. Thus we will know that at least
one of the assumptions we used in the derivation is wrong.
Also, we will see that the proof and its experimental tests have
absolutely nothing to do with Quantum Mechanics.
Now we are ready for the proof itself. First, I assert that:
Number(A, not B, C) + Number(not A, B, not C) must be either 0 or a
positive integer
or equivalently:
Number(A, not B, C) + Number(not A, B, not C) greater than or equal
to 0
This should be pretty obvious, since either no members of the group have
these combinations of properties or some members do.
Now we add Number(A, not B, not C) + Number(A, B, not C) to the
above expression. The left hand side is:
Number(A, not B, C) + Number(A, not B, not C) + Number(not A, B, not
C) + Number(A, B, not C)
and the right hand side is:
0 + Number(A, not B, not C) + Number(A, B, not C)
But this right hand side is just:
Number(A, not C)
since for all members either B or not B must be true. In
the classroom example above, when we counted the number of men without blue
eyes we include both those whose height was over 5' 8" and those whose height
was not over 5' 8".
Above we wrote "since for all members either B or not B
must be true." This will turn out to be important.
We can similarly collect terms and write the left hand side as:
Number(A, not B) + Number(B, not C)
Since we started the proof by asserting that the left hand side is
greater than or equal to the right hand side, we have proved the inequality,
which I re-state:
Number(A, not B) + Number(B, not C) greater than or equal to
Number(A, not C)
We have made two assumptions in the proof. These are:
- Logic is a valid way to reason. The whole proof is an exercise
in logic, at about the level of the "Fun With Numbers" puzzles one sometimes
sees in newspapers and magazines.
- Parameters exist whether they are measured or not. For
example, when we collected the terms Number(A, not B, not C) + Number(A, B,
not C) to get Number(A, not C), we assumed that either not B
or B is true for every member.
APPLYING BELL'S INEQUALITY TO ELECTRON SPIN
Consider a beam of electrons from an electron gun. Let us set the following
assignments for the three parameters of Bell's inequality:
A: electrons are "spin-up" for an "up" being defined as straight
up, which we will call an angle of zero degrees. B: electrons are
"spin-up" for an orientation of 45 degrees. C: electrons are
"spin-up" for an orientation of 90 degrees.
Then Bell's inequality will read:
Number(spin-up zero degrees, not spin-up 45 degrees) + Number(spin-up
45 degrees, not spin-up 90 degrees) greater than or equal to Number(spin-up
zero degrees, not spin-up 90 degrees)
But consider trying to measure, say, Number(A, not B). This is
the number of electrons that are spin-up for zero degrees, but are not
spin-up for 45 degrees. Being "not spin-up for 45 degrees" is, of course,
being spin-down for 45 degrees.
We know that if we measure the electrons from the gun, one-half of them
will be spin-up and one-half will be spin-down
for an orientation of 0 degrees, and which will be the case for an individual
electron is random. Similarly, if measure the electrons with the filter
oriented at 45 degrees, one-half will be spin-down and one-half will be
spin-up.
But if we try to measure the spin at both 0 degrees and 45 degrees
we have a problem.
The figure to the right shows a measurement first at 0 degrees
and then at 45 degrees. Of the electrons that emerge from the first
filter, 85% will pass the second filter, not 50%. Thus for electrons
that are measured to be spin-up for 0 degrees, 15% are spin-down for
45 degrees. |
 |
Thus measuring the spin
of an electron at an angle of zero degrees irrevocably changes the number
of electrons which are spin-down for an orientation of 45 degrees. If
we measure at 45 degrees first, we change whether or not it is spin-up
for zero degrees. Similarly for the other two terms in this application
of the inequality. This is a consequence of the Heisenberg Uncertainty
Principle. So this inequality is not experimentally testable.
In our classroom example, the analogy would be that determining the
gender of the students would change their height. Pretty weird, but true for
measuring electron spin.
However, recall the correlation experiments that we discussed earlier. Imagine
that the electron pairs that are emitted by the radioactive substance
have a total spin of zero. By this we mean that if the right hand electron
is spin-up its companion electron is guaranteed to be spin-down provided the
two filters have the same orientation.
| Say in the illustrated experiment the left hand filter is oriented
at 45 degrees and the right hand one is at zero degrees. If the left
hand electron passes through its filter then it is spin-up for an
orientation of 45 degrees. Therefore we are guaranteed that if we
had measured its companion electron it would have been spin-down for
an orientation of 45 degrees. We are simultaneously measuring the
right-hand electron to determine if it is spin-up for zero degrees.
And since no information can travel faster than the speed of light,
the left hand measurement cannot disturb the right hand measurement. |
 |
So we have "beaten" the
Uncertainty Principle: we have determined whether or not the electron to the
right is spin-up zero degrees, not spin-up 45 degrees by measuring its
spin at zero degrees and its companion's spin at 45 degrees.
Now we can write the Bell inequality as:
Number(right spin-up zero degrees, left spin-up 45 degrees) +
Number(right spin-up 45 degrees, left spin-up 90 degrees) greater than or equal
to Number(right spin-up zero degrees, left spin-up 90 degrees)
This completes our proof of Bell's Theorem.
The same theorem can be applied to measurements of the polarisation of
light, which is equivalent to measuring the spin of photon pairs.
The experiments have been done. For electrons the left polarizer is set
at 45 degrees and the right one at zero degrees. A beam of, say, a billion
electrons is measured to determine Number(right spin-up zero degrees, left
spin-up 45 degrees). The polarizers are then set at 90 degrees/45 degrees,
another billion electrons are measured, then the polarizers are set at 90
degrees/zero degrees for another billion electrons.
The result of the experiment is that the inequality is violated. The
first published experiment was by Clauser, Horne, Shimony and Holt in 1969
using photon pairs. The experiments have been repeated many times
since.
The experiments done so far have been for pairs of electrons, protons,
photons and ionised atoms. It turns out that doing the experiments for photon
pairs is easier, so most tests use them. Thus, in most of the remainder of this
document the word "electron" is generic.
Technical note: You may recall from our discussion of the Stern-Gerlach
experiment that doing a correlation experiment for electrons with the
polarisers at some relative angle is equivalent to doing the experiment for
photons with the polarisers at half the relative angle of the electron
polarisers. Thus, when we discuss an electron measurement with the polarisers
at, say, zero degrees and 45 degrees, for a photon experiment it would be zero
degrees and 22.5 degrees.
In the last section we made two assumptions to derive Bell's inequality
which here become:
- Logic is valid.
- Electrons have spin in a given direction even if we do not measure
it.
Now we have added a third assumption in order to beat the Uncertainty
Principle:
- No information can travel faster than the speed of light.
We will state these a little more succinctly as:
- Logic is valid.
- There is a reality separate from its observation
- Locality.
You will recall the we discussed proofs by negation. The fact that our
final form of Bell's inequality is experimentally violated indicates that at
least one of the three assumptions we have made have been shown to be
wrong.
You will also recall that earlier we pointed out that the theorem and
its experimental tests have nothing to do with Quantum Mechanics. However, the
fact that Quantum Mechanics correctly predicts the correlations that are
experimentally observed indicates that the theory too violates at least one of
the three assumptions.
Finally, as we stated, Bell's original proof was in terms of hidden
variable theories. His assumptions were:
- Logic is valid.
- Hidden variables exist.
- Hidden variables are local.
Most people, including me, view the assumption of local hidden variables
as very similar to the assumption of a local reality.
WHAT NOW?
As can be easily imagined, many people have tried to wiggle out of this
profound result. Some attempts have critiqued the experimental tests. One
argument is that since we set the two polarizers at some set of angles and then
collect data for, say, a billion electrons there is plenty of time for the
polarizers to "know" each other's orientation, although not by any known
mechanism. More recent tests set the orientation of the the polarizers randomly
after the electrons have left the source. The results of these tests are
the same as the previous experiments: Bell's inequality is violated and the
predicted Quantum correlations are confirmed. Still other tests have set the
distance between the two polarizers at 11 km, with results again confirming the
Quantum correlations.
Another critique has been that since the correlated pairs emitted by the source
go in all directions, only a very small fraction of them actually end up being
measured by the polarizers. Another experiment using correlated Beryllium atoms
measured almost all of the pairs, with results again confirmed the Quantum correlations.
There is another objection to the experimental tests that, at least so
far, nobody has managed to get totally around. We measure a spin combination
of, say, zero degrees and 45 degrees for a collection of electrons and then
measure another spin combination, say 45 degrees and 90 degrees, for
another collection of electrons. In our classroom example, this is sort
of like measuring the number of men students whose height is not over 5' 8" in
one class, and then using another class of different students to measure the
number of students whose height is over 5' 8" but do not have blue eyes. The
difference is that a collection of, say, a billion electrons from the source in
the correlation experiments always behaves identically within small and
expected statistical fluctuations with every other collection of a billion
electrons from the source. Since that fact has been verified many many times
for all experiments of all types, we assume it is true when we are doing these
correlation experiments. This assumption is an example of inductive logic; of
course we assumed the validity of logic in our derivation.
Sometimes one sees statements that Bell's Theorem says that information
is being transmitted at speeds greater than the speed of light. So far I have
not seen such an argument that I believe is correct. If we are sitting by either
of the polarisers we see that one-half the electrons pass and one-half do not;
which is going to be the case for an individual electron appears to be random.
Thus, the behavior at our polariser does not allow us to gain any information
about the orientation of the other polariser. It is only in the correlation
of the electron spins that we see something strange. d'Espagnat uses the word
influence to describe what may be traveling at superluminal speeds.
Imagine we take a coin and carefully saw it in half so that one piece is
a "heads" and the other is a "tails." We put each half in a separate envelope
and carry them to different rooms. If we open one of the envelopes and see a
heads, we know that the other envelope contains a tails. This correlation
"experiment" corresponds to spin measurements when both polarisers have the
same orientation. It is when we have the polarisers at different orientations
that we see something weird.
So far we don't know which of the assumptions we made in the proof are
incorrect, so we are free to take our pick of one, two or all three. We shall
close this section by briefly considering the consequences of discarding the
assumption of the validity of logic and then the consequences of discarding the
assumption of a reality separate from its observation. In the next section we
shall explore the idea of a non-local universe.
What If Logic Is Invalid?
It has been suspected since long before Bell that Quantum Mechanics is
in conflict with classical logic. For example, deductive logic is based on a
number of assumptions, one of which is the Principle of the Excluded Middle:
all statements are either true or false.
But consider the following multiple choice test question:
- The electron is a wave.
- The electron is a particle.
- All of the previous.
- None of the above.
From wave-particle duality we know that both statements 1 and 2 are both sort
of true and sort of false. This seems to call into question the Principle of
the Excluded Middle. Thus, some people have worked on a multi-valued logic that
they hope will be more consistent with the tests of Bells' Theorem and therefore
with Quantum Mechanics. Gary Zukav's The Dancing Wu Li Masters has a
good discussion of such a quantum logic; since numerous editions of this book
exist and every chapter is numbered 0, I can't supply a more detailed
reference.
Mathematics itself can be viewed as just a branch of deductive logic, so if
we revise the rules of logic we will need to devise a new mathematics
You may be interested to know that deductive logic has proved that logic is
incomplete. The proof was published in 1931 by Gödel; a good reference
is Hofstader's Gödel, Escher, Bach. The key to Gödel's work
is self-reference; we shall see an example of self-reference in the next
sub-section. What he proved was that any mathematics at all, unless it is trivially
limited, will contain statements that are neither true nor false but simply
unprovable.
|
By self-reference we mean a statement or set of statements that
refer to themselves. For example, consider:
This statement is false.
Note that if this statement is true, then it must be false. If the
statement if false, then it must be true. So we have a chain of True »
False » True » False .... |

New Yorker, Mar 5, 2001, pg.
78. |
|
This may remind you a bit of a simple buzzer, such as a door
buzzer.
A buzzer is shown to the right. A flexible piece of metal is bent
into a double L shape and nailed to a board. A big nail is placed just
under the right hand part of the metal, and the metal is adjusted so that it
does not quite touch the big nail. A battery is wired in such a fashion that
when the the metal L is at rest, the circuit is just completed, which
causes the big nail to become an electromagnet. |
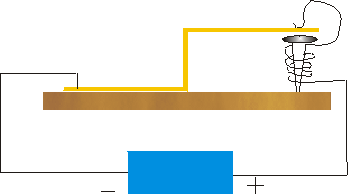 |
This of course pulls the metal down, which breaks the circuit. Thus the
metal springs back up, which completes the circuit again, which pulls the metal
down, and so on. Thus, if the circuit is closed, it opens, and if the circuit
is open, then it is closed. Or, we say we have a chain of Closed »
Open » Closed » Open .... The difference between this example
and the previous self-referential statement is that here the oscillations in
value are occurring in time. You may access a Flash animation of a buzzer by clicking here.
In the late nineteenth century the logician Hilbert used to say "Physics
is too important to be left to the physicists." In retaliation, J.A. Wheeler
has stated: "Gödel is too important to be left to the mathematicians."
Finally, although deductive logic is fairly well understood,
nobody has succeeded in codifying iron-clad rules for inductive logic
that work consistently. Mills tried very hard to do this, but the following
story by Copi shows one problem:
"A favorite example used by critics of the Method of Agreement is the
case of the Scientific Drinker, who was extremely fond of liquor and got drunk
every night of the week. He was ruining his health, and his few remaining
friends pleaded with him to stop. Realizing himself that he could not go on, he
resolved to conduct a careful experiment to discover the exact cause of his
frequent inebriations. For five nights in a row he collected instances of a
given phenomenon, the antecedent circumstances being respectively scotch and
soda, bourbon and soda, brandy and soda, rum and soda, and gin and soda [ugh!].
Then using the Method of Agreement he swore a solemn oath never to touch soda
again!"
Reference: I. Copi, Introduction to Logic, 2nd ed., (Macmillan,
New York, 1961), pp 394-395.
Note the "hidden variable" in the above story.
What If There Is No Reality Separate From Its Observation?
As we have seen, the title of this sub-section is very similar to asking
what are the consequences of having no hidden variables. We shall concentrate
on the first form of the question.
You may have already noticed that the question is a variation on the old
philosophical saw regarding a tree that falls in the forest with nobody there
to hear the sound.
A conflict between the assumption of reality and Quantum Mechanics has
been suspected long before Bell. For example, in referring to the trajectory of
the electron in, say, the double slit experiment Heisenberg stated "The path of
the electron comes into existence only when we observe it."
People have long known that any measurement disturbs the thing being
measured. A crucial assumption of classical sciences has been that at least in
principle the disturbance can be made so small that we can ignore it. Thus,
when an anthropologist is studying a primitive culture in the field, she
assumes that her presence in the tribe is having a negligible effect on the
behavior of the members. Sometimes we later discover that all she was measuring
was the behavior of the tribe when it was being observed by the anthropologist.
Nonetheless, classically we assume a model where we, as
observers, are behind a pane of glass where see what is going on "out
there." Now we suggest that the pane of glass has been shattered. Wheeler
suggests that we should drop the word observer entirely, and replace it
with participator.
Wheeler has thought more deeply on the consequences of a participatory
universe than anybody. He devised the figure to the right, whose
caption is:
“Symbolic representation of the Universe as a self-excited
system brought into being by ‘self-reference’. The universe
gives birth to communicating participators. Communicating participators
give meaning to the universe … With such a concept goes the
endless series of receding reflections one sees in a pair of facing
mirrors.”
Reference: J.A. Wheeler in Isham et al., eds, Quantum Gravity (Clarendon,
Oxford, 1975), pg. 564-565. The colors were used by Wheeler in a
colloquium in the Dept. of Physics, Univ. of Toronto some years
ago. |
 |
You may have noticed a similarity between this view of Quantum Mechanics
and the Idealist philosophy of Bishop Berkeley. Berkeley would likely have been
very happy about Bell's Theorem. Dr. Johnson was, of course, opposed to
Berkeley and used to argue against his philosophy by bellowing "I refute it
thus!" while kicking a large rock. Apparently Johnson found sufficient comfort
from his argument that he didn't mind hurting his foot.
d'Espagnat also tends to believe that the reality assumption is
incorrect. Thus he wrote: "The doctrine that the world is made up of objects
whose existence is independent of human consciousness turns out to be in
conflict with quantum mechanics and with facts established by experiment."
In a participatory universe, I can argue that you owe your objective
existence to my kind intervention in allowing you into my own consciousness.
Thus, there is an inherent solipsism in this position. Wigner was one of
many who was greatly troubled by this.
NON-LOCALITY AND DAVID BOHM
Recall that David Bohm set off in the early 1950's on a quest for the
hidden variables. Nobody has explored the consequences of such variables being
non-local more deeply than Bohm, and in the first sub-section below we shall
discuss some of his work on this topic. In the next sub-section we shall
discuss his later thinking about the nature of the world.
The Implicate Order
A good reference for the material of this sub-section is David Bohm,
Wholeness and the Implicate Order. Although very deep the book is not
technical except for Chapter 4, which I think should not have been included.
Bohm called our everyday world of space, time and causality the
explicate order. He proposed that underlying this everyday world is an
interconnected one which he calls the implicate order. He used a number
of analogies and images to discuss these two orders.
In one analogy he imagined a large cylindrical glass container of
glycerine mounted on a turntable. We place a spot of black ink in the
glycerine. We slowly rotate the container, and the ink gradually disperses
throughout the glycerine. If we slowly rotate the cylinder in the opposite
direction the spot of ink gradually re-forms. When the ink is dispersed it is
in an implicate state: it exists throughout the glycerine. When the ink is a
spot it is explicate: it exists in one part of the glycerine but not in the
other parts. If we continue rotating the cylinder in this opposite direction
the spot disperses again.
We extend the image as follows. We place the spot of ink as before. We
slowly rotate the cylinder one revolution, and the ink has begun to disperse.
We place a second spot of ink just beside where the first spot was, and rotate
for one more revolution. A third spot is placed beside where the second was,
one more revolution, and we continue this for a few spots. Then we continue
slowly rotating the cylinder until all the ink is fully dispersed. When we
reverse the direction of rotation we see the last spot coalesce, then the next
to last one right beside the last one, and so on. We could interpret what we
are seeing as a single spot of ink that is moving. So in the implicate fully
dispersed state we have enfolded the motion in space and time of an object
throughout the glycerine. Reversing the rotation unfolds the reality back into
space and time.
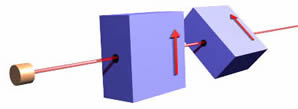
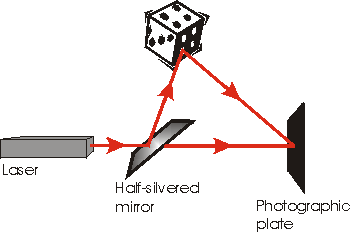 Another analogy is a hologram. As shown
to the right, to make a hologram we split a laser beam into two pieces with a
half-silvered mirror. One piece goes straight to a photographic plate, the
other bounces off the object and then goes to the plate. In order to
reconstruct the image of the object we shine a laser beam through the developed
plate: the three-dimensional image appears. Note that in some sense the
hologram on the plate is an interference pattern between the beam that has
experienced the thing and the beam that experienced no-thing.
Another analogy is a hologram. As shown
to the right, to make a hologram we split a laser beam into two pieces with a
half-silvered mirror. One piece goes straight to a photographic plate, the
other bounces off the object and then goes to the plate. In order to
reconstruct the image of the object we shine a laser beam through the developed
plate: the three-dimensional image appears. Note that in some sense the
hologram on the plate is an interference pattern between the beam that has
experienced the thing and the beam that experienced no-thing.
One characteristic of a hologram is that down to at least a few grains
of the silver in the plate, each piece of the plate contains the entire image.
If we cut the plate in half we do not lose half the image; instead we lose
resolution and the image becomes more fuzzy. Thus each piece of the plate
contains the entire space of the object in an enfolded way; this is an analogy
to the implicate order. When we reconstruct the image, we have unfolded the
implicate order into an explicate one.
There are "multiplexed" holograms that contain time information too. If
the object is moving, we rotate the photographic plate. When we reconstruct the
image if we look from different angles we see the object's motion. Here the
object's time behavior is also enfolded into the totality.
We see that in the implicate order there is no spatial or time
separation. Thus it is a non-local order.
Here is another image used by Bohm:
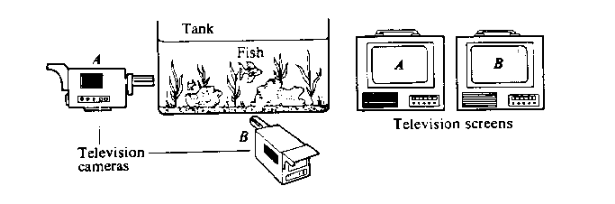
He comments: "The images on the screens are two dimensional
projections (or facets) of a three dimensional reality. ... Yet, since
these projections exist only as abstractions, the three-dimensional reality
is neither of these. ... What is actually found [in the experimental
tests of Bell's theorem] is that the behavior of the two [electrons] is
correlated in a way that is rather similar to that of the two television images
of the fish, as described earlier. Thus ... each electron acts as if it were a
projection of a higher-dimensional reality. ... What we are proposing here is
that the quantum property of a non-local, non-causal relation of distant
elements may be understood through an extension of the notion described above."
-- pg. 187-188.
The following table compares the explicate and implicate order:
| Explicate |
Implicate |
| parts make up the whole |
whole makes up the parts |
| spatial separation |
holographic |
| describable |
"finger pointing to the moon" |
| things exist |
'thing' and 'no-thing' interfere |
| "ten thousand things" |
illusion |
| spacetime |
spectra |
Given the unbroken wholeness of the implicate order, Bohm asked why our
thought is so dominated by fragmentation.
"... fragmentation is continually being brought about by the almost
universal habit of taking the content of our thought for `a description of the
world as it is'." -- pg. 3.
He also wrote about what to do about this:
"[Meditation] is particularly important because ... the illusion that
the self and the world are broken into fragments originates in the kind of
thought that goes beyond its proper measure and confuses its own product with
the same independent reality. To end this illusion requires insight, not only
into the world as a whole, but also into how the instrument of thought is
working." -- pg. 25.
Bohm's Ontology of Quantum Mechanics
In philosophy, epistemology is the study of what we know and how
we know it; this is as opposed to ontology which studies what actually
exists. Most interpretations of Quantum Mechanics have been developed by people
sympathetic to the idea of a participatory universe; we discussed this idea
above. Therefore, these interpretations are essentially epistemology.
For Bohm, this wasn't good enough. He developed an ontology in his later
years. His master work, The Undivided Universe, was written with his
collaborator B.J. Hiley and published in 1993. It is written for physicists,
and I can't really recommend it to a non-technical audience. Here we shall
briefly explore some of the conclusions from this book.
Essentially, Bohm and his school re-interpreted the mathematics of
Quantum Mechanics and extracted a part of the equation which they called the
quantum potential. The quantum potential is non-local, and is
responsible for all the non-local effects predicted by the theory.
The quantum potential guides, say, the path of an electron in a way
similar to the way a radio beacon can guide an airplane coming in for a landing
at the airport. It is the jets, ailerons, rudder, etc. on the plane that
mechanically determines where the plane is going, but the beacon guides the
way.
In Bohm's ontology electrons really are particles. For the case of, for example,
the double slit experiment for electrons, each electron goes through either
the upper slit or the lower slit; it has a definite path independent of its
observation. However, the quantum potential is different depending on whether
the other slit is open or closed; since this potential is non-local it can instantaneously
change if the other slit is opened or closed. Thus the electron paths are different
depending on whether or not the other slit is open.
You may recall that for a chaotic system, very small changes in
initial conditions leads to radically different trajectories; you may read more
about this
here.
It turns out that for the double slit experiment for electrons, the motion of
the electron after it has passed the slits is chaotic in just this sense. Thus,
even small thermal fluctuations in the electron's interaction with the slits
cause the electron's future motion to be unknowable to us, even though it is
strictly deterministic. Thus it seems to us that the path of the electron is
random, although in reality it is not.
We call Physics before Quantum Mechanics classical; thus the
theories of relativity are classical. Usually we characterise a classical
theory as one that includes observers and strict determinism, while a
non-classical theory has participators and randomness. If Bohm's interpretation
is correct we need to change the way we characterise the distinction. A
classical theory is local, while a non-classical one is non-local; both are
strictly deterministic and have observers. Bohm had some hope that his ontology
would have experimentally testable consequences, although no such experiments
have yet been done.
You may wish to know that in Bohm's analysis the so-called photon is not
a particle; it is an electromagnetic field whose particle-like behavior arises
because of its interaction with the quantum potential.
Note that in this work, then, Bohm has finally identified the hidden
variable he searched for for so many years: it is the quantum potential.
The non-locality of this potential led Bohm to invoke an image very
similar to the one Wheeler used above in his discussion of the universe as a
self-excited system:
"Classical physics provided a mirror that reflected only the objective
structure of the human being who was the observer. There is no room in this
scheme for his mental process which is thus regarded as separate or as a mere
'epiphenomenon' of the objective processes. ... [Through the] mirror [of
quantum physics] the observer sees 'himself' both physically and mentally in
the larger setting of the universe as a whole. ... More broadly one could say
that through the human being, the universe is making a mirror to observe
itself." -- Bohm and Hiley, The Undivided Universe, pg. 389
A colleague remarked to me that Bohm's heroic attempts to keep a reality
separate from its observation, in this "final" form, is worse than the
alternative of not having a reality. I don't know about the word worse,
but after Bell's theorem something has to give, whether it is reality, locality
and/or logic itself.
There are still some unresolved issues regarding Bohm's ontology. For
example, as discussed
elsewhere,
the standard planetary model of the atom where the electrons orbit the nucleus
just as the planets orbit the Sun is impossible, because according to classical
electromagnetism such an electron is in a state of non-uniform accelerated
motion and must radiate away its energy, causing it to spiral into the nucleus.
However, when we think about the electron in its wave aspect, then when the
waves are in a standing wave pattern, this corresponds to the allowed orbits of
the Bohr model and the electrons do not radiate.
When the idea of treating the electron as a wave is fully developed by
Quantum Mechanics, the orbits are more complicated then indicated in the
document referenced in the previous paragraph.
|
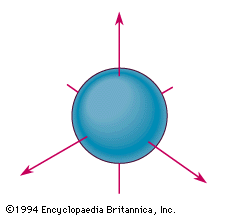
To the right we show the "wave function" for the electron in its
ground state orbital. It can be seen that it is spherically symmetric. In an
earlier discussion we called this the orbit for which the quantum number
n is equal to 1.
In Bohm's ontology, the electron is a particle. But for this orbit
the electron is stationary, with the electric force trying to pull it into the
proton being just balanced by the quantum potential. Thus, this electron will
certainly not radiate away energy. |
 |
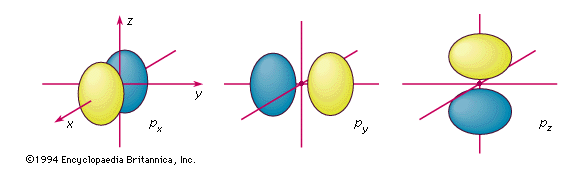 |
|
For the state with principle quantum number 2, there is a
spherically symmetric wave function that looks just like the one shown before
for n = 1. But there are also three other orbitals, which look as shown
above.
For the first two of these "p" orbitals, the electrons are moving
and accelerating and would be expected to radiate away energy. The last
pz orbital turns out to represent an electron that is
stationary.
This is clearly in conflict with the fact that the electrons in
the atom do not radiate energy except when they change from one allowed orbit
to another allowed orbit. |
In fact, this difficulty manifests in another form in the double slit experiment
for electrons. If the electron is a particle that changes its trajectory when
it goes through the slits, it too should radiate away energy. One of Bohm's
colleagues, Vigier, recently said that the wavelength of this radiation is very
large and so the energy loss is negligible; some people believe that Vigier
is wrong. Work on this problem is currently being pursued; one of the people
working on it is Professor John Sipe of this Department. I became aware of this
controversy in attempting to find the answer to a question asked by former JPU200Y
student Sharmilla Reid.
CELLULAR AUTOMATA
A cellular automaton provides another approach to the study of the
emergence of structures based on rules.
One of the best known automata is the Game of Life, devised by John
Conway in 1970. This example is played on a large checkerboard-like grid. One
starts with a configuration of cells on the board that are populated, and then
calculates the population in succeeding generations using three simple rules:
- Birth: an unoccupied cell with exactly 3 occupied neighbors
will be populated in the next generation.
- Survival: an occupied cell with 2 or 3 occupied neighbors
will be populated in the next generation.
- Death: in all other cases a cell is unoccupied in the next
generation.
Despite the simplicity of the rules, truly amazing patterns of movement, self-organising
complexity, and more arise in this game.
To the right is a Flash animation of the simplest possible
configuration that changes from generation to generation but never grows
or dies out.
- Click on the Step button to step from generation
to generation. In this mode the number of occupied neighbors of each
cell is shown.
- Click on Play to resume playing the animation.
There are many resources available on the web to explore this fascinating
"game" in more detail.
If you are reading the pdf version of this document,
Flash animations are not available from pdf. |
|
It has been proposed that these sorts of automata may form a useful model for
how the universe really works. Contributors to this idea include Konrad Zuse
in 1967, Edward Fredkin in the early 1980's, and more recently Stephen Wolfram
in 2002. Wolfram's work in particular is the outcome of nearly a decade of work,
which is described in a mammoth 1200 page self-published book modestly titled
A New Kind of Science.
There are two key features of cellular automata that are relevant for this
discussion:
- The rules are always strictly deterministic.
- The evolution of a cell depends only on its nearest neighbors.
This seems to put a cellular automaton model of Physics in conflict with Bell's
Theorem, which asserts that a logical local deterministic model of the universe
can not be correct.
Advocates of the cellular automaton model attempt to argue that there is no
essential conflict, just an apparent one. Arguments include:
- That the apparent randomness of quantum phenomena is only pseudo-random.
To me, they seem to be re-introducing the idea of hidden variables
via the back door. Plamen Petrov in one of the proponents of this argument.
- That there is some sort of higher-dimensional thread outside of the normal
four dimensions of space and time. This "thread" will somehow allow
for super-luminal connections. Wolfram and others have proposed this idea.
- Other Wolfram supporters have argued that the speed of light is or can be
much greater than the "usual" value that we are used to. Whether
or not it needs to be infinite is not clear.
In the previous Bohm's Ontology of Quantum Mechanics sub-section,
we saw that Bohm's attempt to keep causality ended up with a totally non-local
mechanism encapsulated in a Quantum Potential. Even there, we saw at
the end that there are serious problems with the model.
It may be that there are even more serious problems with the Cellular Automaton
model for the way the universe works. The controversy continues to be very active
as of this writing (Spring, 2003). A semi-random list of further readings is:
FINALLY ...
Einstein died many years ago, and so is not here to defend himself against
claims of what he would or would not do today. Nonetheless, I tend to think
that if he were alive today, Bell's theorem would force him to accept Quantum
Mechanics.
AUTHOR
This document was written in February 1999 by David M. Harrison, Department
of Physics, University of Toronto, harrison@physics.utoronto.ca.
This is version 1.27 of the document, date (m/d/y) 03/17/06.
This document is Copyright © 1999 - 2004 David M. Harrison.



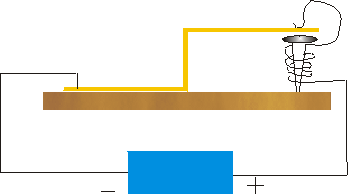

 Another analogy is a hologram. As shown
to the right, to make a hologram we split a laser beam into two pieces with a
half-silvered mirror. One piece goes straight to a photographic plate, the
other bounces off the object and then goes to the plate. In order to
reconstruct the image of the object we shine a laser beam through the developed
plate: the three-dimensional image appears. Note that in some sense the
hologram on the plate is an interference pattern between the beam that has
experienced the thing and the beam that experienced no-thing.
Another analogy is a hologram. As shown
to the right, to make a hologram we split a laser beam into two pieces with a
half-silvered mirror. One piece goes straight to a photographic plate, the
other bounces off the object and then goes to the plate. In order to
reconstruct the image of the object we shine a laser beam through the developed
plate: the three-dimensional image appears. Note that in some sense the
hologram on the plate is an interference pattern between the beam that has
experienced the thing and the beam that experienced no-thing.