A Non-Mathematical Proof of Gravitational Time
Dilation
Click here to go to the
UPSCALE home page.
Click
here to go to the
JPU200Y home page.
Click
here to go to the
Physics Virtual Bookshelf.
Author
This document was written in February 2002 by David M. Harrison, Dept.
of Physics, Univ. of Toronto, mailto:harrison@physics.utoronto.ca.
This document is Copyright © 2002 David M. Harrison.
This is $Revision: 1.1 $, $Date: 2002/02/08 20:23:19 $ (year/month/day UTC).
Introduction
Einstein's General Theory of Relativity predicts that clocks in a
gravitational fields run slow compared to clocks not in gravitational field,
and that the stronger the gravitational field the slower the clock runs. In
this little document, we "derive" the existence of the effect without
mathematics. First we will do a careful re-examination of the Equivalence
Principle, and then do the derivation.
The Equivalence Principle
Einstein's Equivalence Principle states that accelerations are
equivalent to gravitational fields. This means that there is no experiment in a
fairly small sized room that you can do to determine which one of the following
two circumstances are true:
- The room is on the surface of the Earth, where the acceleration due
to gravity is down and equal to 9.8 m/s2.
- The room is on a rocket ship in free space that is accelerating
upwards at 9.8 m/s2.
Here we will explore what the phrase "fairly small sized room"
means.
|
We imagine that we are in the room, and have two balls, as shown
to the right. They are fixed to the ceiling by means of clamps. At some moment
in time both clamps simultaneously release the balls. |
 |
|
|
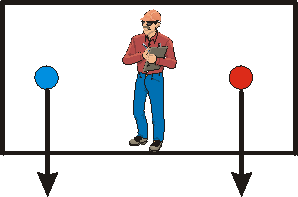
If the room is on a rocket ship that is accelerating upwards at
9.8 m/s2 with respect to some inertial frame of reference in free
space, then relative to us the balls will fall straight down, accelerating at
9.8 m/s2, until they strike the floor of the room. Thus the distance
between the balls remains constant while they are falling. |
 |
|
|
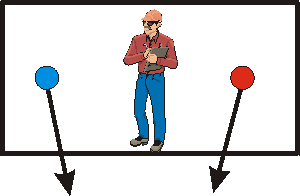
However, as you may know, objects on the surface of the Earth are
attracted gravitationally to the point right at the center of the Earth. Thus
if the room were on the Earth, the balls would not fall quite straight down,
but would fall to the center of the Earth. The figure to the right exaggerates
the magnitude of the effect. The distance between the balls decreases while
they are falling. |
 |
|
|
If we align the two balls vertically in the centre of the room and
drop them, they will both fall straight down whether the room is on the Earth
or on the rocket. However, on the rocket they will both accelerate downwards at
exactly 9.8 m/s2 relative to us. The acceleration due to
gravity on the Earth, however, decreases as the distance from the centre or the
Earth increases. Thus the upper (blue) ball will accelerate at a rate slightly
less than the lower (red) one, and the distance between the two balls will
increase by a small amount while they are both falling |
 |
Thus, given sufficiently sensitive instruments we can tell the
difference between being on the rocket and being on the Earth. Does this mean
that the Equivalence Principle is wrong? No. It does mean, though, that it is
only strictly true in an infinitesimally small region of space. The word for
this property is local, and we conclude that the Equivalence Principle
is only truly locally.
The Proof
|
We imagine we have two clocks, labelled 1 and 2,
that are fixed and stationary relative to the surface of the Earth. We are in a
reference frame that is in free fall towards the surface of the earth, and we
have our own clock, stationary with respect to us. Note that since we are in
free fall, we are floating.
According to the Equivalence Principle, our reference frame is
inertial, and therefore our clock can do good measurements of time. Note that
any other clock, stationary relative to us, at some other location is not
necessarily doing good measurements of time, since the Equivalence Principle is
only true locally. Thus we will compare the rates of the Earth clocks to ours
only when we pass right by them.
When we pass by Clock 1, it is moving with respect to us.
Therefore, Special Relativity tells us that it is running slowly relative to
our clock. Similarly when we pass by Clock 2, since it is moving with respect
to us it will be running slowly compared to our clock. |
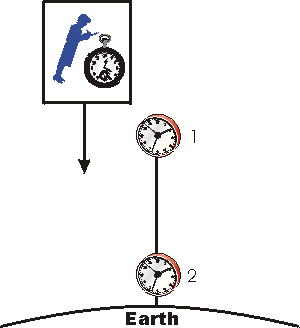 |
But, since we are in free fall our speed with respect to the Earth and
the two Earth-bound clocks is increasing: we are accelerating down at 9.8
m/s2 relative to the Earth. So when we pass Clock 2, its speed with
respect to us is greater than the speed of Clock 1 when we passed by it.
Thus, for us in our good inertial reference frame we conclude that Clock
2 is running more slowly than Clock 1. So the clock in the stronger
gravitational field, Clock 2, runs more slowly than the clock in the weaker
gravitational field
This completes the derivation of the fact that clocks in gravitational
fields run slowly.




