Click here to go
to the Physics Virtual Bookshelf.
Click here to go to the UPSCALE
home page.
This document is a non-mathematical introduction to waves, harmonics, and standing waves.
"Pongileoni's bowing and the scraping of the anonymous fiddlers had shaken the air in the great hall, had set the glass of the windows looking on to it vibrating: and this in turn had shaken the air in Lord Edwards' apartment on the further side. The shaking air rattled Lord Edwards' membrana typani; the interlocked malleus, incus, and stirrup bones were set in motion so as to agitate the membrane of the oval window and raise an infinitesimal storm in the fluid of the labyrinth. The hairy endings of the auditory nerve shuddered like weeds in a rough sea; a vast number of obscure miracles were performed in the brain, and Lord Edwards ecstatically whispered `Bach!'" -- Aldous Huxley, Point Counter Point.
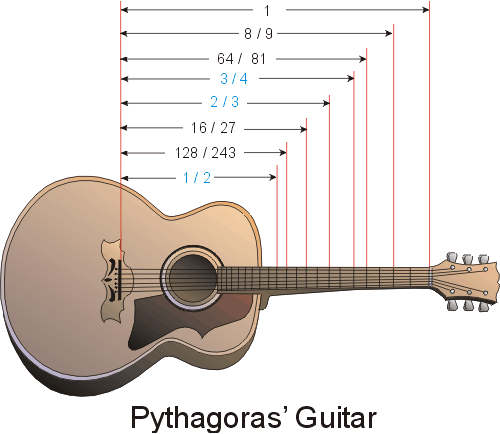
Pythagoras and his school did experiments to discover the relations between musical notes.The pitch of a note being played on, say, a guitar depends on:
Pressing the finger onto the string clamps the string onto the metal fret to the left of where the finger is pressed. The effective length of the string become the distance between the fret and the bridge on the left hand side. If we say the length of the string is one in some system of units, we show the effective lengths of the string for each of the notes in the scale. These harmonious "consonant" lengths were discovered by Pythagoras.

The lengths are related to each other by the ratios of whole integers. In fact, the Pythagoreans believed that this was a general principle of the universe: everything is related by the ratios of whole integers. Thus, the cosmos sings in harmony, the "Music of the Spheres."
The Pythagoreans also discovered the existence of irrational numbers. For example, the square root of 2 is:
1.414213562...
The ellipsis (...) indicates that the decimals never end or repeat. There are no integers i and j for which i/j equals the square root of two. These irrational numbers were considered such a blot on the perfection of the universe that knowledge of their existence was suppressed.
 |
The universe as a monochord, by Fludd, 1627. From Heninger, The Cosmographical Glass, pg 133. |
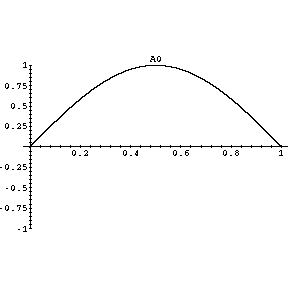
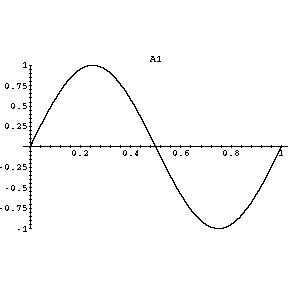
If a string is fixed on both ends, then the only waves that can occur are those with zero amplitude at those fixed ends; such points of zero amplitude are called nodes. Below we show four of the infinite number of vibrations with a node at each end. These vibrations are called standing waves.
 |
 |
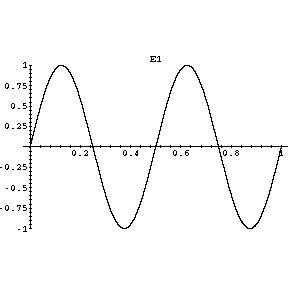 |
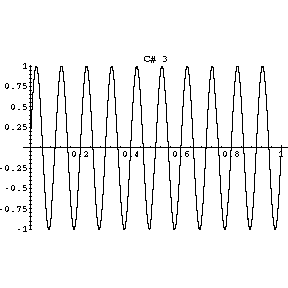 |
You may animate any of the above four images by clicking on it. If you are using a relatively modern browser, the animation will appear in a separate window; close that window whenever you wish. If you are using an older browser, the animation will appear in this window; to return here, use the Back button on your browser.
The first mode determines the note the string is tuned to. It is the fundamental mode of vibration for the string. All of the higher order vibrations are called by musicians the "overtones". The relative amount of the overtones determines the musical timbre that distinguishes, say, a violin and a guitar that are playing the same note.
If the string's tension, material and length is such that the first vibration shown, labeledA0, is vibrating at 440 Hz, then the string is playing the note Concert A.
The next allowed vibration, labeledA1, has a a distance between adjacent nodes of exactly one-half of the distance of the A0 one. Thus, this vibration will be at 880 Hz, which is the note A one octave above Concert A. The next shown standing wave, labeledE1, will produce the note E, while the last shown standing wave will produce the note C#. Musicians will recognise that these notes make up the A chord.
Most of the allowed overtones for a vibrating string generate one of the notes of the chord, while others represent the minor seventh, the ninth, etc. of the chord.
The ear takes the complicated sound wave from, say, a musical instrument and measures the relative amounts and phases of the overtones; the brain then recombines this information into a perception of the timbre of the note.
We have just seen that the complex vibration of a string can be represented as a sum of the fundamental vibration and the overtones. Fourier proved that any vibration can be similarly be represented. We illustrate by building up a so-called "sawtooth" shaped wave, which looks like this:
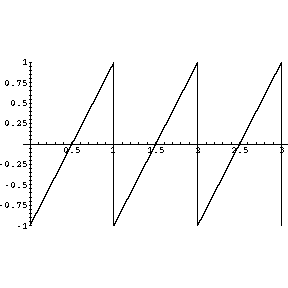
We now take the fundamental and the first harmonic and add them. For those with color monitors, the fundamental is in green and the harmonic is in blue. The sum of these two is in red.
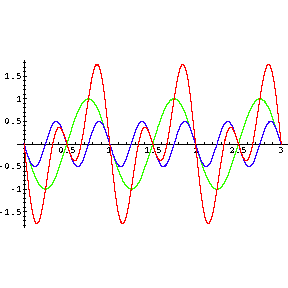
The sum of the two vibrations in the above graphic looks roughly like the sawtooth. We now take that sum, represented now in green, plus the next overtone in blue and show the sum of these as the red line:
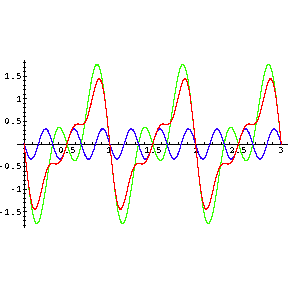
The above is clearly getting closer to the desired shape. Finally, we jump to showing the fundamental plus the first 9 overtones. This clearly looks even closer. We can get as close as we wish to the desired sawtooth shape by adding more and more overtones.
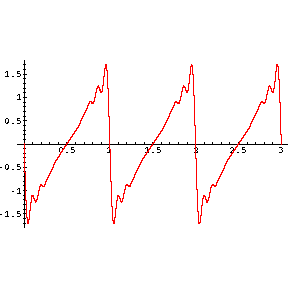
|
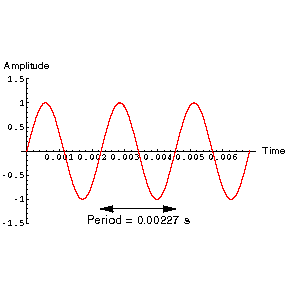
Here is a somewhat more musical example of the same theorem. The figure to the right shows the amplitude versus time for a sine wave, which we imagine is oscillating at 440 Hz. As shown, this corresponds to the wave repeating its motion every 0.00227 seconds; this number is called the period of the oscillation. You may listen to a 24k wav format file playing that note by clicking here. This is a fairly dull, "electronic" sound. Technical note: one over the period is the frequency. In this case, then, 1/0.00227 = 440. |
 |
|
The figures to the right shows a single period of that simple sine wave, plus four "overtones;" the relative amplitudes of the four waves is not arbitrary. For a 440 Hz fundamental vibration, the overtones occur at 2 × 440 = 880 Hz, 3 × 440 = 1320 Hz, 4 × 440 = 1760 Hz, 5 × 440 = 2200 Hz, 6 × 440 Hz = 2640 Hz, etc. You might notice that the 2200 Hz vibration is missing from the group to the right. |
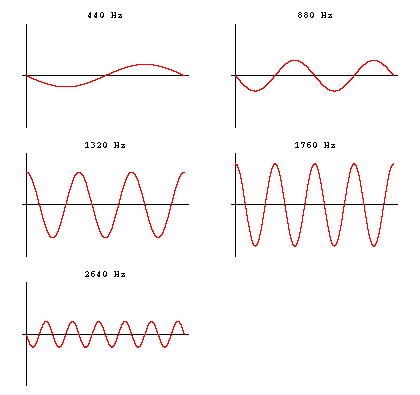 |
|
This figure shows the sum of those five simple waves. A 24k wav file of the sound wave that looks like the lower figure is available here. With some imagination you might think it sounds a little bit like an oboe. Adding more overtones could make it sound more like a real oboe. For comparison, a 71k wav file of a real oboe is available here. |
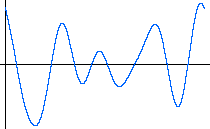 |
Whether it sounds like an oboe or not, though, the overtones are clearly adding a timbre to the note, making it more interesting.
Even this "simple" wave form, with only five vibrations, shows some fairly complex behavior. Each overtone is vibrating at a different frequency from the other overtones and the tonic. If the sound wave is vibrating in time as shown above, that oscillation is related to a wave traveling by in space. A 51k animation of a wave traveling from left to right in space and the corresponding vibration in time at a particular place is available here. By "following the bouncing ball" you can see that there are times when the five sinusoidal vibrations combine to give a relatively large total amplitude, while at other times they tend to cancel each other out, giving a relatively small total amplitude. This is responsible for the "quiver" you may have noticed in the synthesized oboe-like tone above.
You may wish to know that the relative amounts and phases of the fundamental and overtones in the above example were determined by sampling a recording of an actual oboe playing the note Concert A.
You may view an animation of any of the four images above by clicking on it. Just as for the previous animations, in a modern browser the animation will be in a separate window while older browsers will show it in this window.
One thing to notice in the above is that the overtones are not related to the fundamental mode via harmonic ratios of whole numbers. For example, the first overtone is vibrating at 1.59334... times the fundamental. Thus, although drums are tuned to a note corresponding to the first shown mode, the overtones are not related musically to the fundamental and thus the drum sounds "percussive"
The banjo's distinctive sound comes because it combines the harmonic overtones from its vibrating string with the percussive overtones from its drum head.
Some stringed instruments, such as the banjo or sitar, have drone strings which sometimes or usually are not directly played. However the sound waves and/or vibrations of the instrument itself causes those strings to vibrate in resonance with the notes that are actually being played.
A particularly dramatic example of resonance occurred on November 7, 1940 when a breeze excited a resonance in a new bridge at Tacoma Narrows, Washington, causing the bridge to collapse. An mpeg video clip of the bridge oscillating in resonance is available here; total file size is about 700k.
If you have access to a real piano, you may do some experiments on resonance and standing waves.
Press slowly and then hold down the key of a bass note, say G2; no sound is produced but the damper remains lifted off that string. Then hit hard and staccato the key of the note one octave above, G3. After the sound from that string has stopped you will hear the G2 string sounding G3. Repeat by hitting the twelfth, D4, C4, B4 etc. If you hit, say, A3 there will be no effect. This is because A3 is not an upper harmonic of G2.
Again lift the damper of the G2 string. Simultaneously strike D4, G4 and B4. After their sound has disappeared it is possible to hear the G2 string vibrating in all three modes simultaneously. Thus that one string is playing a full G major triad.
Again lift the damper of the G2 string. Hit with your right underarm all black and white keys of two or more octaves above G3. After the initial burst has decayed the G2 string vibrates beautifully in the dominant seventh chord G3, D4, G4, B4, D5, F5, G5, …
We have now shown that a given string can vibrate in different modes. Now we will prove that a string, sounded normally, does vibrate in many harmonic modes. Pick a bass note, such as G2 but slowly press and hold the G3 key. Then sound a loud staccato G2. The G3 string starts vibrating in its own fundamental mode G3. The reason is it has been excited by the first overtone of the vibrating G2 string. Similarly, you may excite resonances in the keys D4, G4, B4, D5, … etc. Each one will be excited by the corresponding overtones of the G2 string.
Above we showed the placing of frets on a guitar if it had been built by a Pythagorean. Such a guitar would play beautifully in some keys, but not in others! The relationship between musical notes is called the temperament. A Flash document exploring this further has been prepared. It requires that your computer have the Flash player of at least Version 6, and that you have sound. The demonstration has a file size of 151k and will appear in a separate window: to access it click here.
Juan G. Roeder, Introduction to the Physics and Psycholophysics of Music, 3rd ed. (Springer Verlag, 1995), ISBN: 0387943668.
This book has hardly any mathematics, but a wealth of information on not only the topics of this "page" but a great deal more. Highly recommended.
This document was written by David M. Harrison, Dept. of Physics, Univ. of Toronto, harrison@physics.utoronto.ca in December 1999.
This document is Copyright © 1999, 2000 David M. Harrison. This is version 1.12, date (m/d/y) 03/24/03.
This material may be distributed only subject to the terms and conditions set forth in the Open Content License, v1.0 or later (the latest version is presently available at http://opencontent.org/opl.shtml).